>    read "HermiteCT.mm";

>    with(HermiteCT);

[HermiteReduction, HermiteTelescoping, KernelReduction, PolynomialReduction, ShellReduction]

 

Calling sequence:

                           HermiteReduction(H, y)
          Input:  H,  a hyperexponential function in y;
                     y,  a variable name;

          Output: [u, r, T],   u and r are rational functions in y and T a hyperexponential function

                                      with certificate differential-reduced such that

                                                      H = Dy(u*T) + r*T,

                                       where r is the residual form of the shell of H.


Example 1 for HermiteReduction

>    f1 := 1/(y-1)^2;

f1 := 1/((y-1)^2)

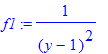
>    HermiteReduction(f1, y);

[-1/(y-1), 0, 1]

Example 2 for HermiteReduction

>    f2 := sqrt(y^2+1)/(y-1)^2;

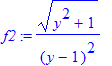
f2 := (y^2+1)^(1/2)/(y-1)^2

>    HermiteReduction(f2, y);

[-1/2*(y+1)/(y-1), 1/2*y*(y+1)/(y-1)/(y^2+1), (y^2+1)^(1/2)]


Calling sequence:
                          HermiteTelescoping(H, x, y, Dx, 'T')
             Input: H,       a bivariate hyperexponential function;

                      x, y,     two variable names;
                        Dx,    a operator name.
            Output: L,     a linear differential operator in Dx over F(x) and
                                the fifth argument 'T' is a bivariate hyperexponential
                                function such that


                                  L(x, Dx)(H) = Dy(T).

         T is of the form  [r, exp(int(udx + vdy)]
          with r a rational function and v differential-reduced w.r.t. y.

Example 1 for HermiteTelescoping

>    h1 := diff(sqrt(x-2*y)*exp(x^2*y), y);

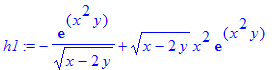
h1 := -1/(x-2*y)^(1/2)*exp(x^2*y)+(x-2*y)^(1/2)*x^2*exp(x^2*y)

>    ZT1 := DETools[Zeilberger](h1, x, y, Dx);

ZT1 := [1, (x-2*y)^(1/2)*exp(x^2*y)]

>    HT1 := HermiteTelescoping(h1, x, y, Dx, 'T1'); 

The estimated order of minimal telescopers is 1 

 

HT1 := 1

 Check whether two methods get the same minimal telescoper (up to a univariate rational function in F(x)).

>    degree(normal(ZT1[1]/HT1), Dx);  

0

>    T1;

[x-2*y, 1/(x-2*y)^(1/2)*exp(x^2*y)]

Example 2  for HermiteTelescoping

>    h2 := sqrt(x-2*y)*exp(x^2*y);

h2 := (x-2*y)^(1/2)*exp(x^2*y)

>    ZT2 := DETools[Zeilberger](h2, x, y, Dx);

ZT2 := [-3*x^3+6+2*Dx*x, -(x-2*y)^(1/2)*(3*x-4*y)*exp(x^2*y)]

>    HT2 := HermiteTelescoping(h2, x, y, Dx, 'T2'); 

The estimated order of minimal telescopers is 1 

 Check order 1

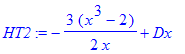
HT2 := -3/2*(x^3-2)/x+Dx

>    degree(normal(ZT2[1]/HT2), Dx);

0

Example 3  for HermiteTelescoping

>    h3 := (1+x+4*x*y)/(11+x+y^2+x*y);

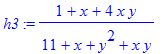
h3 := (1+x+4*x*y)/(11+x+y^2+x*y)

>    ZT3 := DETools[Zeilberger](h3, x, y, Dx):

>    HT3 := HermiteTelescoping(h3, x, y, Dx, 'T3'); 

The estimated order of minimal telescopers is 2 

 Check order 1 

Check order 2

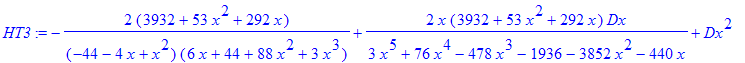
HT3 := -2*(3932+53*x^2+292*x)/(-44-4*x+x^2)/(6*x+44+88*x^2+3*x^3)+2*x*(3932+53*x^2+292*x)/(3*x^5+76*x^4-478*x^3-1936-3852*x^2-440*x)*Dx+Dx^2

>    degree(normal(ZT3[1]/HT3), Dx);

0

Example 4  for HermiteTelescoping

>    h4 := 1/sqrt(y*(y-1)*(y-x));

h4 := 1/((y*(y-1)*(y-x))^(1/2))

>    ZT4 := DETools[Zeilberger](h4, x, y, Dx);

ZT4 := [1+(4*x^2-4*x)*Dx^2+(8*x-4)*Dx, 2*y*(y-1)/(-y+x)/(-y*(y-1)*(-y+x))^(1/2)]

>    HT4 := HermiteTelescoping(h4, x, y, Dx, 'T4'); 

The estimated order of minimal telescopers is 2 

 Check order 1 

Check order 2

HT4 := 1/(4*x*(x-1))+(2*x-1)/x/(x-1)*Dx+Dx^2

>    degree(normal(ZT4[1]/HT4), Dx);

0

Example 5  for HermiteTelescoping

>    h5 := sqrt(x-2*y)*exp(x^2*y);

h5 := (x-2*y)^(1/2)*exp(x^2*y)

>    ZT5 := DETools[Zeilberger](h5, x, y, Dx);

ZT5 := [-3*x^3+6+2*Dx*x, -(x-2*y)^(1/2)*(3*x-4*y)*exp(x^2*y)]

>    HT5 := HermiteTelescoping(h5, x, y, Dx, 'T5'); 

The estimated order of minimal telescopers is 1 

 Check order 1

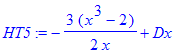
HT5 := -3/2*(x^3-2)/x+Dx

>    degree(normal(ZT5[1]/HT5), Dx);

0